About Fibonacci : Fungsi Rekursif dan Dynamic Programming Sederhana - part 2

بسم الله الرحمن الرحيم

Di posting sebelumnya telah dibahas identitas penting dari barisan Fibonacci, yaitu relasi rekurens yang biasa dikenal \[F_{n}=F_{n-1}+F_{n-2}\]

Kita akan membahas lebih lanjut relasi ini dan menentukan cara untuk menghitung barisan Fibonacci ini.

Bagi yang belum tahu tentang Fibonacci silahkan lihat post sebelumnya: About Fibonacci : Menghitung Kelinci - part 1

Relasi Rekurens

Sekilas relasi rekurens intinya adalah menggunakan fungsi yang sama dalam pemanggilan fungsi, seperti \(L_{n}=L_{n-1}+2n-1\). Terlihat bahwa di dalam fungsi \(L_{n}\) ada fungsi \(L_{n-1}\). Dengan kata lain nilai fungsi parameter N bergantung pada fungsi yang sama dengan parameter N-1. Dan juga relasi rekursif berguna mengubah problem yang besar menjadi problem yang lebih kecil. Fibonacci ke-N menjadi Fibonacci ke-(N-1) dan ke-(N-2). Kurang lebih seperti itu cara kerja fungsi rekursif.

Dalam pendefinisian fungsi rekursif ada 2 hal yang harus diperhatikan : basis dan rekurens.

• Basis bisa dikatakan kondisi awal dari fungsi rekurens. Ketika fungsi telah punya nilai di suatu parameter tertentu, itulah yang disebut basis. Basis bisa lebih dari satu nilai, bisa hanya memiliki satu nilai. Intinya basis ini yang jadi titik berhentinya pemanggilan fungsi.
• Rekurens adalah pemanggilan fungsi yang menuju basis dengan memanggil dirinya sendiri. Ketika nilai fungsi belum ada, maka kita gunakan rekurens untuk memanggil fungsi serupa yang menuju basis. Jika masih belum di basis, pemanggilan rekurens akan terus dilakukan sampai bertemu basis.

Contoh pada suku ke-N Fibonacci yaitu F(n) = F(n-1) + F(n-2). Bagian ini dinamakan rekurens fungsi.

Sedangkan untuk menentukan basis kita lihat bahwa fungsi di atas berhenti saat F(3) = F(2) + F(1), karena tidak mungkin dilakukan pemanggilan F(1) = F(0) + F(-1) karena bilangan Fibonacci terkecil yaitu bilangan ke-1 yaitu 1 (ada juga yang mendefinisikan bilangan Fibonacci dimulai Fibonacci ke-0 yaitu 0). Maka kita ambil basisnya F(1) = 1 dan F(2) = 1. (atau F(1) = 1 dan F(0) = 0 jika menggunakan definisi Fibonacci ke-0).

Dengan memanfaatkan definisi rekursif ini kita bisa implementasikan Fibonacci ke-N dengan fungsi rekursif seperti berikut.

function fibonacci (n : integer) : integer;
begin
   if n<3 then
      fibonacci := 1           { basis : suku pertama dan kedua bernilai 1 }
   else
      fibonacci := fibonacci(n-1)+fibonacci(n-2); { rekurens }
end;

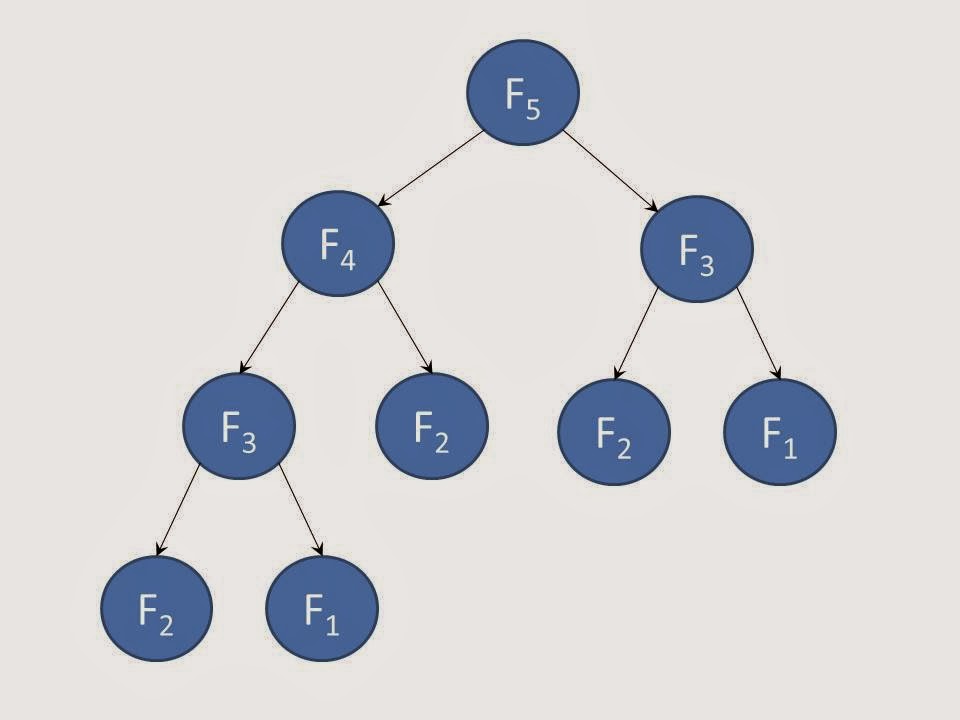
Tapi ada kelemahan dalam pemanggilan fungsi seperti ini. Coba perhatikan skema pemanggilan fungsi di bawah!

Setiap pemanggilan F(n) akan memanggil F(n-1) dan F(n-2) meskipun F(n-2) juga telah dipanggil pada penghitungan F(n-1). Gambar di atas menunjukkan dalam pemanggilan F(5) saja F(3) dipanggil berulang-ulang, yaitu 2 kali. Begitupun dengan F(1) dan F(2). Coba bayangkan jika F(500) dipanggil! Maka F(1) dan F(2) akan dipanggil ribuan kali. Betapa tidak efektifnya program kita!!

Maka kita bisa menggunakan alternatif lain yaitu dengan memakai teknik Dynamic Programming.

Dynamic Programming (DP)

Kelemahan kita menggunakan rekursif biasa yang baru saja dibahas yaitu terjadinya overlapping subproblem, yaitu subproblem yang telah dihitung dicari lagi sehingga pemanggilan fungsi menjadi sangat boros. Dengan DP kelemahan rekursif yang satu ini bisa tercover.

Inti dari DP adalah mengubah parameter menjadi state fungsi dan menyimpan setiap state yang dilalui fungsi dalam suatu struktur data. Sehingga sekali kita telah menghitungnya kita tidak perlu mengulanginya lagi.

Dalam membuat konstruksi DP kita dapat memakai 2 cara : top-down dan bottom-up.

1. DP Top-Down
Style yang satu ini cukup mudah. Dengan menggunakan fungsi rekursif yang sebelumnya dan sedikit modifikasi maka akan terbentuk DP top-down.

Jika kita lihat, kelemahan rekursi yang sebelumnya hanyalah pada kurangnya penyimpanan state sehingga menyebabkan overlap. Maka sekarang kita akan menyimpan nilai semua state F(n) pada suatu variabel (misal array) yang kita namakan variabel memo sehingga kita tidak perlu menghitung berulang-ulang. Metode ini disebut memoization/memoisasi.

Coba perhatikan ilustrasi di bawah!

Dengan menyimpan nilai state nilai F(3) bisa dimanfaatkan langsung tanpa menghitung lagi dari F(2) dan F(1). Kurang lebih implementasinya DP top-down seperti berikut.

var fibo : array[1..1000] of integer;   { variabel memo }
{ anggap array fibo telah diinisiasi nilai 0 }

function fibonacci (n : integer) : integer; { fungsi rekursif }
begin
   if n<3 then 
      fibonacci := fibo[n] := 1
   else if fibo[n]=0 then
           fibonacci := fibo[n] := fibonacci(n-1)+fibonacci(n-2)
        else
           fibonacci := fibo[n];
end;

2. DP Bottom-Up
Jika DP top-down membuat solusi dengan fungsi rekursif (yang cenderung mengecil ke basis), maka DP bottom-up membuat solusi dari basis lalu membesar ke state berikutnya sampai batas yang diinginkan. Bisa dikatakan style ini kebalikan dari style sebelumnya.

Coba perhatikan ilustrasi berikut!

Dari gambar terlihat bahwa relasi rekursif F(n) = F(n-1) + F(n-2) digunakan untuk membangun solusi F(3), F(4), dan seterusnya hingga F(8). Dimulai dari basis F(1) dan F(2), solusi ini membangun solusi hingga F(n) yang diinginkan.

Implementasinya cukup dengan iterasi biasa untuk mengisi F(3) sampai F(n) sehingga masih cukup mudah dibuat. Dan karena implementasinya bebas rekursi maka untuk Fibonacci dengan urutan yang sangat besar (contoh: F(2000,000,000)) tidak akan mengalami stack overflow ketika pemanggilannya seperti terjadi pada fungsi rekursi. Inilah keunggulan utama DP bottom-up dibanding top-down. Meskipun kadang implementasi bottom-up umumnya lebih susah dari top-down karena dimulai dari basis dan pemilihan rekurens yang harus ekstra hati-hati (karena bisa jadi tidak semua parameter memo digunakan dalam DP). Pengalaman saya sendiri saat ICPC kemarin tim saya harus bergelut selama hampir sejam untuk mendebug solusi DP bottom-up karena ada bagian yang harusnya tidak dimasukkan rekurens ternyata belum dikecualikan.

Kurang lebih implementasinya seperti berikut.

var fibo : array[1..1000] of integer;   { variabel memo }

begin {program utama}
   fibo[1]:=1;    { inisiasi basis }
   fibo[2]:=1;
   for i:=3 to n do   { pengisian memo dengan iterasi }
       fibo[i]:=fibo[i-1]+fibo[i-2];
   { output fibo[n] jika perlu }
end.

Dan perlu diketahui untuk kedua solusi DP di atas memiliki kompleksitas \(O(N)\), yaitu linear terhadap nilai N. Sehingga untuk N < 100 juta, runtime yang dibutuhkan masih sekitar 1 detik atau kurang.

Untuk N yang sangat besar kita tidak dapat memakai solusi ini karena pasti akan mendapat verdict TLE karena runtime yang dibutuhkan bisa 100 detik atau malah jauh lebih besar. Maka ada cara yang lebih baik menggunakan teknik Divide and Conquer dengan perkalian matriks.
Tunggu di post berikutnya : 
About Fibonacci : Divide and Conquer Approach; Matrix Exponentiation- part 3

About Fibonacci : Menghitung Kelinci - part 1

بسم الله الرحمن الرحيم

Kita semua pasti sudah tau apa itu barisan Fibonacci. Yaitu barisan yang sukunya adalah jumlah 2 suku sebelumnya. Tapi kenapa bisa gitu dan gimana problem ini muncul ? Coba simak narasi di bawah.

Misal kita beli seekor anak kelinci. Anak kelinci itu akan dewasa setelah setahun. Lalu pada tahun berikutnya kelinci dewasa tadi akan melahirkan seekor anak kelinci. Tiap tahun si kelinci dewasa akan melahirkan anak terus-menerus. Dan si anak kelinci ini akan mengikuti pola yang sama dengan induknya. Dewasa setelah setahun lahir, lalu melahirkan seekor anak tiap tahun -dengan asumsi kelinci tidak akan mati dan beranak tanpa pasangan selamanya hihi

Jika kita lihat polanya, anak kelinci pada tiap tahun :

Pada tahun pertama, 1 ekor (anak kelinci yang baru dibeli)

Pada tahun kedua, 1 ekor (anak kelinci sudah dewasa)

Pada tahun ketiga, 2 ekor (kelinci dewasa melahirkan seekor anak)

Pada tahun keempat, 3 ekor (kelinci dewasa melahirkan seekor anak dan si anak kelinci yang tadi sudah dewasa)

dan seterusnya yang dapat kita simpulkan menjadi

1, 1, 2, 3, 5, 8, 13, 21 ...

Ternyata pola yang didapat yaitu jumlah kelinci pada tahun ini adalah kelinci pada tahun lalu ditambah kelinci dua tahun lalu. Kok bisa?

Coba diingat lagi, kelinci bisa melahirkan ketika dia sudah berumur minimal 2 tahun.
Maka jumlah kelinci dewasa saat ini sejumlah kelinci dewasa tahun lalu plus kelinci yang dilahirkan tahun lalu yang baru saja dewasa.
\[D_{n} = D_{n-1} + A_{n-1} = F_{n-1}\]
Lalu jumlah kelinci muda sekarang sejumlah kelinci dewasa dua tahun lalu dan jumlah kelinci yang baru dewasa tahun lalu/kelinci muda dua tahun lalu. 
\[A_{n} = D_{n-2} + A_{n-2} = F_{n-2}\]
Maka jumlah kelinci sekarang = jumlah kelinci muda sekarang + jumlah kelinci dewasa sekarang.
\[F_{n}=D_{n} + A_{n}= F_{n-1} + F_{n-2}\]

Pembuktian sudah beres. Sekarang kita coba terapkan pola ini ke salah satu soal OSK 2013 (bidang informatika) yang telah dimodif sedemikian rupa. Check this out!!

---

Sebuah katak berada pada salah satu sisi sungai ingin menyeberangi sungai dengan melewati 5 buah batu yang berada di sepanjang aliran sungai (lihat gambar di bawah). Katak ingin menghitung berapa kemungkinan cara yang dia gunakan untuk menyeberangi sungai. Karena katak jago melompat, katak mampu melompat dari batu satu ke batu sebelahnya, atau melompati satu batu tersebut dan mendarat di sampingnya lagi. Coba bantu katak menghitung berapa kemungkinan langkah yang diambil untuk bisa ke ujung satunya!

Jawab :

Coba kita lihat jumlah cara yang bisa diambil untuk mendarat di batu ke-n

Pada batu ke-1 : hanya 1 cara
Pada batu ke-2 : karena bisa dari batu pertama atau dari ujung, maka jumlah cara ada 1+1=2 cara
Pada batu ke-3 : idem di atas, 2+1=3 ( coba cari tahu kenapa 2+1 :) )
Pada batu ke-4 : ada 3+2=5 cara
Pada batu ke-5 : ada 3+5=8 cara
Dan ke ujung kanan ada 8+5=13 cara.

Simpel kan :). Meski begitu banyak masalah dalam bidang ilmu komputer yang melibatkan perhitungan bilangan Fibonacci. Misal, dalam perhitungan kompleksitas algoritma Euclid dalam mencari GCD (Greatest Common Divisor), pembentukan struktur data Fibonacci, dan beberapa masalah komputasi lainnya.

Perlu diketahui meskipun barisan Fibonacci termasuk barisan yang tidak tentu (karena tergantung suku-suku sebelumnya), tapi rasio \(\frac{F_{n+1}}{F_{n}}\) akan mendekati suatu nilai yang disebut Phi / Golden Ratio. Dengan menggunakan Golden Ratio ini kita dapat menghitung barisan Fibonacci secara langsung tanpa harus tahu suku-suku sebelumnya. Tapi kita tidak akan menggunakan ini karena dalam pemrograman perhitungan nilai real (bilangan non bulat) rawan menghasilkan nilai yang salah dalam pembulatan. Dan juga pemrosesan bilangan real cenderung lebih lambat dibanding bilangan bulat.

Lalu bagaimana cara menghitung Fibonacci dengan cepat? Tunggu postingan berikutnya :
About Fibonacci : Fungsi Rekursif dan Dynamic Programming Sederhana - part 2

Barbershop, Antara Masyarakat Kritis dan Mahasiswa Apatis

بسم الله الرحمن الرحيم

Sebenarnya ini tejadi ketika liburan belum berakhir dan saya masih di kota buaya. Berawal ketika rambut shaggy ku semakin tidak karuan. Ibu saya yang notabene perfeksionis -kayaknya hampir semua ibu gitu- memaksa saya untuk potong rambut. Maka saya pun melangkah bersama adik saya yang agak besar ke barber shop langganan saya.

Seperti biasa disana benar-benar ramai. Bukan hanya karena yang datang banyak dan hanya dilayani dua orang. Tapi memang banyak hal yang jadi perbincangan. Terutama karena menjelang pemilu April besok, banyak opini tentang politik bertaburan di ruangan itu.

Ada yang bilang percuma milih caleg itu. Buat kampanye aja udah sekian miliar. Kalau terpilih apa ndak ingin balik bondo (Jawa; arti : balik modal).

Ada lagi kalau salah satu gubernur DKI yang sekarang sedang populer itu kerjanya cuma pencitraan. Tiap blusukan mesti ada wartawan. Tapi itu dibantah orang yang bilang kalau itu ancaman untuk pihak-pihak yang tidak ingin berbenah dan cuma makan gaji buta.

Intinya kepekaan masyarakat masih terasa di ruangan itu. Di beberapa tempat lain seperti warung kopi, warung nasi, dan pangkalan ojek atau becak sering saya juga mendengar perbincangan serupa. Membuktikan bahwa masyarakat kita masih kritis dalam melihat realita yang terjadi.

Jujur, saya melihat bahwa sebagai mahasiswa -orang yang harusnya lebih terpelajar- kita kurang mengamati dan berdiskusi. Wawasan kita harusnya lebih terbuka karena kita telah belajar lebih banyak dari mereka. Dan tanggung jawab kita untuk peka dan lebih responsif terhadap kebutuhan masyarakat.

Jadi masih mau tidak peduli?